The slides are here..
Our seventh class meeting will focus on Chapter 9 and Chapter 11 of Handbook of Regression Modeling in People Analytics.
The Skinny
Two major topics: survival analysis with some discussion of parametric survival analysis and power and study planning.
Some Models
```{r, message=FALSE, warning=FALSE}
library(haven)
library(tidyverse)
options(scipen=7)
BKT.Data <- read_dta("https://github.com/robertwwalker/xaringan/raw/master/CMF-Week-6/img/bkt98ajps.dta")
cloglog_model <- glm(dispute ~ dem + growth+allies+contig+capratio+trade+as.factor(py),
data = BKT.Data, family=binomial(link = "cloglog"))
summary(cloglog_model)
```
Call:
glm(formula = dispute ~ dem + growth + allies + contig + capratio +
trade + as.factor(py), family = binomial(link = "cloglog"),
data = BKT.Data)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.4183 -0.2282 -0.1420 -0.0828 3.9654
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.113947 0.082348 -13.527 < 2e-16 ***
dem -0.049384 0.007288 -6.776 1.24e-11 ***
growth -0.008082 0.007612 -1.062 0.288357
allies -0.430045 0.078126 -5.504 3.70e-08 ***
contig 0.554479 0.077111 7.191 6.45e-13 ***
capratio -0.003023 0.000405 -7.464 8.39e-14 ***
trade -12.503176 9.960629 -1.255 0.209385
as.factor(py)2 -1.797014 0.130842 -13.734 < 2e-16 ***
as.factor(py)3 -1.910023 0.145076 -13.166 < 2e-16 ***
as.factor(py)4 -2.130485 0.165704 -12.857 < 2e-16 ***
as.factor(py)5 -2.378740 0.193902 -12.268 < 2e-16 ***
as.factor(py)6 -2.836553 0.246354 -11.514 < 2e-16 ***
as.factor(py)7 -2.831567 0.246584 -11.483 < 2e-16 ***
as.factor(py)8 -2.757412 0.239957 -11.491 < 2e-16 ***
as.factor(py)9 -2.701098 0.239710 -11.268 < 2e-16 ***
as.factor(py)10 -2.990651 0.280582 -10.659 < 2e-16 ***
as.factor(py)11 -3.207771 0.319289 -10.047 < 2e-16 ***
as.factor(py)12 -3.077872 0.305041 -10.090 < 2e-16 ***
as.factor(py)13 -3.670483 0.410654 -8.938 < 2e-16 ***
as.factor(py)14 -4.310370 0.578624 -7.449 9.38e-14 ***
as.factor(py)15 -4.329282 0.578841 -7.479 7.48e-14 ***
as.factor(py)16 -3.209284 0.336350 -9.542 < 2e-16 ***
as.factor(py)17 -3.973393 0.501858 -7.917 2.43e-15 ***
as.factor(py)18 -5.339488 1.000841 -5.335 9.55e-08 ***
as.factor(py)19 -3.367405 0.381031 -8.838 < 2e-16 ***
as.factor(py)20 -3.704984 0.449627 -8.240 < 2e-16 ***
as.factor(py)21 -4.552930 0.708058 -6.430 1.27e-10 ***
as.factor(py)22 -4.069630 0.579535 -7.022 2.18e-12 ***
as.factor(py)23 -3.894665 0.579557 -6.720 1.82e-11 ***
as.factor(py)24 -3.761143 0.579762 -6.487 8.73e-11 ***
as.factor(py)25 -17.294682 317.920692 -0.054 0.956617
as.factor(py)26 -2.758181 0.411827 -6.697 2.12e-11 ***
as.factor(py)27 -17.282784 369.870471 -0.047 0.962731
as.factor(py)28 -17.251363 368.516083 -0.047 0.962662
as.factor(py)29 -3.702860 0.709164 -5.221 1.78e-07 ***
as.factor(py)30 -3.209144 0.579970 -5.533 3.14e-08 ***
as.factor(py)31 -4.201176 1.002675 -4.190 2.79e-05 ***
as.factor(py)32 -3.364920 0.710748 -4.734 2.20e-06 ***
as.factor(py)33 -3.869193 1.001648 -3.863 0.000112 ***
as.factor(py)34 -3.112066 0.709943 -4.384 1.17e-05 ***
as.factor(py)35 -3.651929 1.003808 -3.638 0.000275 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 7719.2 on 20989 degrees of freedom
Residual deviance: 5108.1 on 20949 degrees of freedom
AIC: 5190.1
Number of Fisher Scoring iterations: 17
Onset
```{r}
cloglog_model <- BKT.Data %>% filter(contdisp!=1) %>% glm(dispute ~ dem + growth+allies+contig+capratio+trade+as.factor(py),
data = ., family=binomial(link = "cloglog"))
summary(cloglog_model)
```
Call:
glm(formula = dispute ~ dem + growth + allies + contig + capratio +
trade + as.factor(py), family = binomial(link = "cloglog"),
data = .)
Deviance Residuals:
Min 1Q Median 3Q Max
-0.7871 -0.2159 -0.1389 -0.0865 3.7395
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -3.6245986 0.1777915 -20.387 < 2e-16 ***
dem -0.0386198 0.0099036 -3.900 9.64e-05 ***
growth -0.0385768 0.0119971 -3.216 0.001302 **
allies -0.3649215 0.1110691 -3.286 0.001018 **
contig 0.9723362 0.1216458 7.993 1.32e-15 ***
capratio -0.0022631 0.0005188 -4.362 1.29e-05 ***
trade -3.3539539 9.4666133 -0.354 0.723119
as.factor(py)2 0.4397894 0.1883996 2.334 0.019578 *
as.factor(py)3 0.3491778 0.1987540 1.757 0.078946 .
as.factor(py)4 0.1389052 0.2145618 0.647 0.517379
as.factor(py)5 -0.0975959 0.2370175 -0.412 0.680510
as.factor(py)6 -0.5558984 0.2812503 -1.977 0.048095 *
as.factor(py)7 -0.5483215 0.2818479 -1.945 0.051721 .
as.factor(py)8 -0.4806042 0.2759244 -1.742 0.081544 .
as.factor(py)9 -0.4085754 0.2758451 -1.481 0.138560
as.factor(py)10 -0.6910220 0.3121538 -2.214 0.026848 *
as.factor(py)11 -0.9041806 0.3477067 -2.600 0.009311 **
as.factor(py)12 -0.7831121 0.3340890 -2.344 0.019077 *
as.factor(py)13 -1.3767286 0.4329015 -3.180 0.001472 **
as.factor(py)14 -2.0004550 0.5944831 -3.365 0.000765 ***
as.factor(py)15 -2.0216113 0.5948272 -3.399 0.000677 ***
as.factor(py)16 -0.9003473 0.3631977 -2.479 0.013177 *
as.factor(py)17 -1.6627516 0.5202523 -3.196 0.001393 **
as.factor(py)18 -3.0275260 1.0095413 -2.999 0.002709 **
as.factor(py)19 -1.0567304 0.4048386 -2.610 0.009048 **
as.factor(py)20 -1.3950385 0.4701169 -2.967 0.003003 **
as.factor(py)21 -2.2331641 0.7205377 -3.099 0.001940 **
as.factor(py)22 -1.7502751 0.5957590 -2.938 0.003305 **
as.factor(py)23 -1.5705581 0.5959611 -2.635 0.008405 **
as.factor(py)24 -1.4617157 0.5962646 -2.451 0.014228 *
as.factor(py)25 -14.9967931 317.2228798 -0.047 0.962294
as.factor(py)26 -0.4515102 0.4345600 -1.039 0.298802
as.factor(py)27 -14.9541479 369.7841411 -0.040 0.967742
as.factor(py)28 -14.9142319 368.2468025 -0.041 0.967694
as.factor(py)29 -1.3757208 0.7239855 -1.900 0.057406 .
as.factor(py)30 -0.8906066 0.5982936 -1.489 0.136599
as.factor(py)31 -1.9082656 1.0131416 -1.884 0.059631 .
as.factor(py)32 -1.0835368 0.7247409 -1.495 0.134897
as.factor(py)33 -1.6244040 1.0113319 -1.606 0.108229
as.factor(py)34 -0.8541733 0.7242140 -1.179 0.238220
as.factor(py)35 -1.3772737 1.0150861 -1.357 0.174843
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 3978.5 on 20447 degrees of freedom
Residual deviance: 3464.1 on 20407 degrees of freedom
AIC: 3546.1
Number of Fisher Scoring iterations: 17
First Disputes
```{r}
cloglog_model <- BKT.Data %>% filter(prefail<1) %>% glm(dispute ~ dem + growth+allies+contig+capratio+trade+as.factor(py),
data = ., family=binomial(link = "cloglog"))
summary(cloglog_model)
```
Call:
glm(formula = dispute ~ dem + growth + allies + contig + capratio +
trade + as.factor(py), family = binomial(link = "cloglog"),
data = .)
Deviance Residuals:
Min 1Q Median 3Q Max
-0.7128 -0.1614 -0.1095 -0.0698 3.7773
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -3.2093911 0.2016389 -15.917 < 2e-16 ***
dem -0.0455530 0.0131726 -3.458 0.000544 ***
growth -0.0223993 0.0171905 -1.303 0.192574
allies -0.4214307 0.1604019 -2.627 0.008605 **
contig 1.0825191 0.1698031 6.375 0.000000000183 ***
capratio -0.0019172 0.0005997 -3.197 0.001390 **
trade -3.2025168 11.4758988 -0.279 0.780195
as.factor(py)2 -1.2527718 0.3220541 -3.890 0.000100 ***
as.factor(py)3 -1.2831387 0.3341382 -3.840 0.000123 ***
as.factor(py)4 -0.9510071 0.2958496 -3.214 0.001307 **
as.factor(py)5 -1.0081832 0.3134476 -3.216 0.001298 **
as.factor(py)6 -1.3507511 0.3638693 -3.712 0.000205 ***
as.factor(py)7 -1.1691777 0.3347485 -3.493 0.000478 ***
as.factor(py)8 -1.3653452 0.3636651 -3.754 0.000174 ***
as.factor(py)9 -1.9204272 0.4706184 -4.081 0.000044910633 ***
as.factor(py)10 -1.7188749 0.4339540 -3.961 0.000074648813 ***
as.factor(py)11 -1.6925367 0.4347329 -3.893 0.000098898140 ***
as.factor(py)12 -1.8485066 0.4706172 -3.928 0.000085714102 ***
as.factor(py)13 -2.0798172 0.5209821 -3.992 0.000065488374 ***
as.factor(py)14 -2.7004581 0.7210249 -3.745 0.000180 ***
as.factor(py)15 -2.7411325 0.7223353 -3.795 0.000148 ***
as.factor(py)16 -1.6212847 0.4340875 -3.735 0.000188 ***
as.factor(py)17 -2.2723949 0.5956942 -3.815 0.000136 ***
as.factor(py)18 -3.3616368 1.0101302 -3.328 0.000875 ***
as.factor(py)19 -1.5533472 0.4342661 -3.577 0.000348 ***
as.factor(py)20 -2.6625609 0.7226586 -3.684 0.000229 ***
as.factor(py)21 -2.5936447 0.7211901 -3.596 0.000323 ***
as.factor(py)22 -3.2100540 1.0115565 -3.173 0.001507 **
as.factor(py)23 -3.0265595 1.0118712 -2.991 0.002780 **
as.factor(py)24 -2.2142451 0.7234813 -3.061 0.002209 **
as.factor(py)25 -16.4306211 544.9228267 -0.030 0.975946
as.factor(py)26 -0.9809132 0.4732985 -2.073 0.038218 *
as.factor(py)27 -16.3946549 631.3575269 -0.026 0.979283
as.factor(py)28 -16.3579874 627.5407480 -0.026 0.979204
as.factor(py)29 -1.7629611 0.7257339 -2.429 0.015132 *
as.factor(py)30 -1.3099003 0.6006145 -2.181 0.029188 *
as.factor(py)31 -2.3177601 1.0147203 -2.284 0.022363 *
as.factor(py)32 -1.4627978 0.7270825 -2.012 0.044233 *
as.factor(py)33 -2.0042293 1.0133072 -1.978 0.047939 *
as.factor(py)34 -1.2537774 0.7265579 -1.726 0.084412 .
as.factor(py)35 -1.8006874 1.0175421 -1.770 0.076786 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2183.3 on 16990 degrees of freedom
Residual deviance: 1897.1 on 16950 degrees of freedom
AIC: 1979.1
Number of Fisher Scoring iterations: 18
Taylor Smoothing
```{r}
cloglog_model <- BKT.Data %>% filter(prefail<1) %>% glm(dispute ~ dem + growth+allies+contig+capratio+trade+poly(py, 3),
data = ., family=binomial(link = "cloglog"))
summary(cloglog_model)
```
Call:
glm(formula = dispute ~ dem + growth + allies + contig + capratio +
trade + poly(py, 3), family = binomial(link = "cloglog"),
data = .)
Deviance Residuals:
Min 1Q Median 3Q Max
-0.6249 -0.1580 -0.1094 -0.0818 3.7823
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -4.9452420 0.1576014 -31.378 < 2e-16 ***
dem -0.0450710 0.0131444 -3.429 0.000606 ***
growth -0.0269900 0.0171645 -1.572 0.115850
allies -0.4246004 0.1602099 -2.650 0.008043 **
contig 1.0788756 0.1698279 6.353 0.000000000211 ***
capratio -0.0019260 0.0006007 -3.206 0.001344 **
trade -3.0060629 11.5462355 -0.260 0.794594
poly(py, 3)1 -57.1154511 10.9618803 -5.210 0.000000188465 ***
poly(py, 3)2 55.4155210 10.6438428 5.206 0.000000192596 ***
poly(py, 3)3 -5.0958348 9.9455269 -0.512 0.608389
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2183.3 on 16990 degrees of freedom
Residual deviance: 1941.7 on 16981 degrees of freedom
AIC: 1961.7
Number of Fisher Scoring iterations: 9
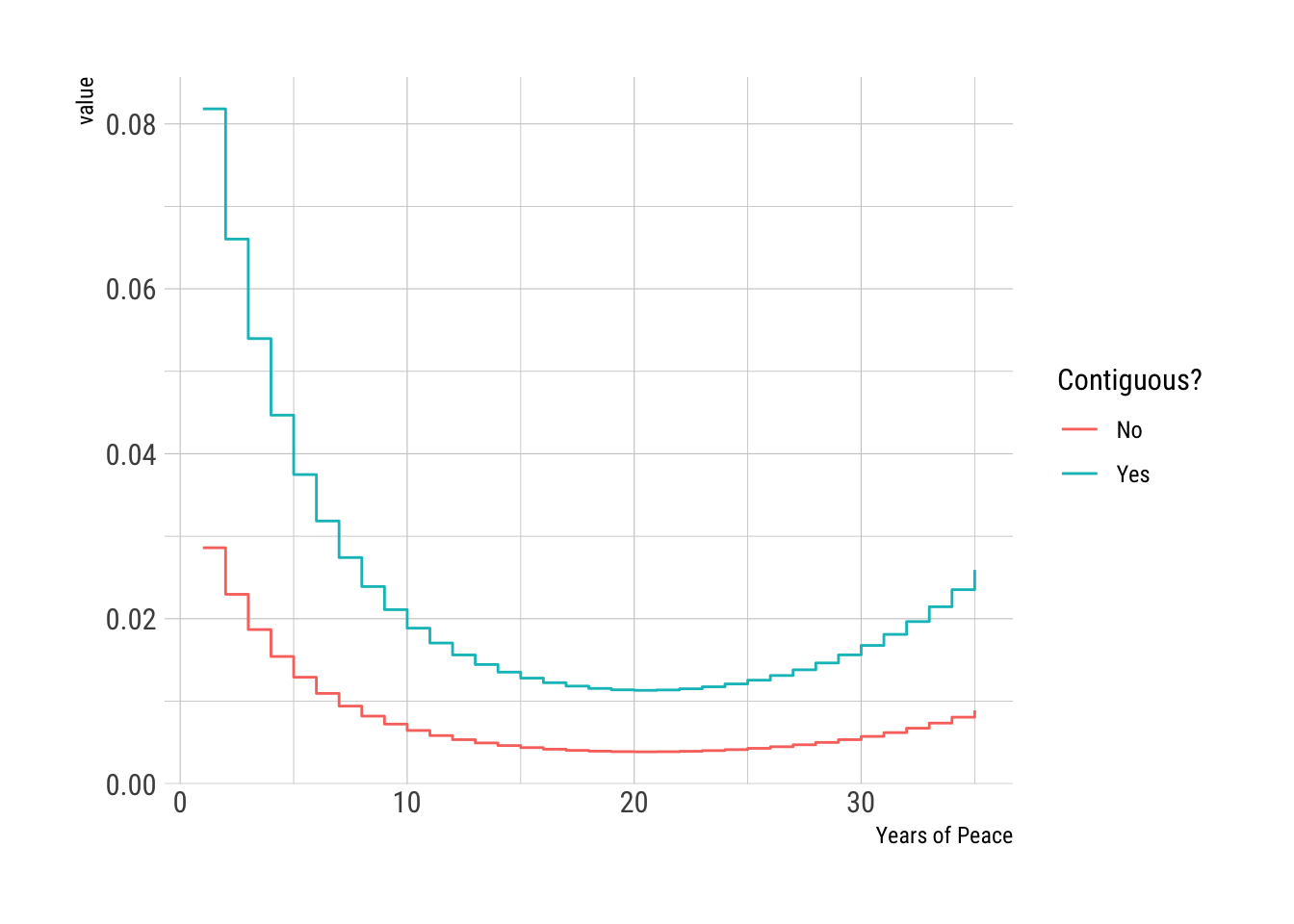
A plot of the baseline hazard.
```{r}
Scenario.1 <- data.frame(dem = 0, growth=0, allies=0, contig=0, capratio=1, trade=0.002, py=seq(1,35))
Scenario.2 <- data.frame(dem = 0, growth=0, allies=0, contig=1, capratio=1, trade=0.002, py=seq(1,35))
Res.1 <- predict(cloglog_model, newdata=Scenario.1, type= "response")
Res.2 <- predict(cloglog_model, newdata=Scenario.2, type= "response")
data.frame(No = Res.1, Yes = Res.2, Scenario.1) %>% pivot_longer(., cols=c(No, Yes)) %>% ggplot() + aes(x=py, y=value, color=name) + labs(x="Years of Peace", color="Contiguous?") + geom_step() + hrbrthemes::theme_ipsum_rc()
```
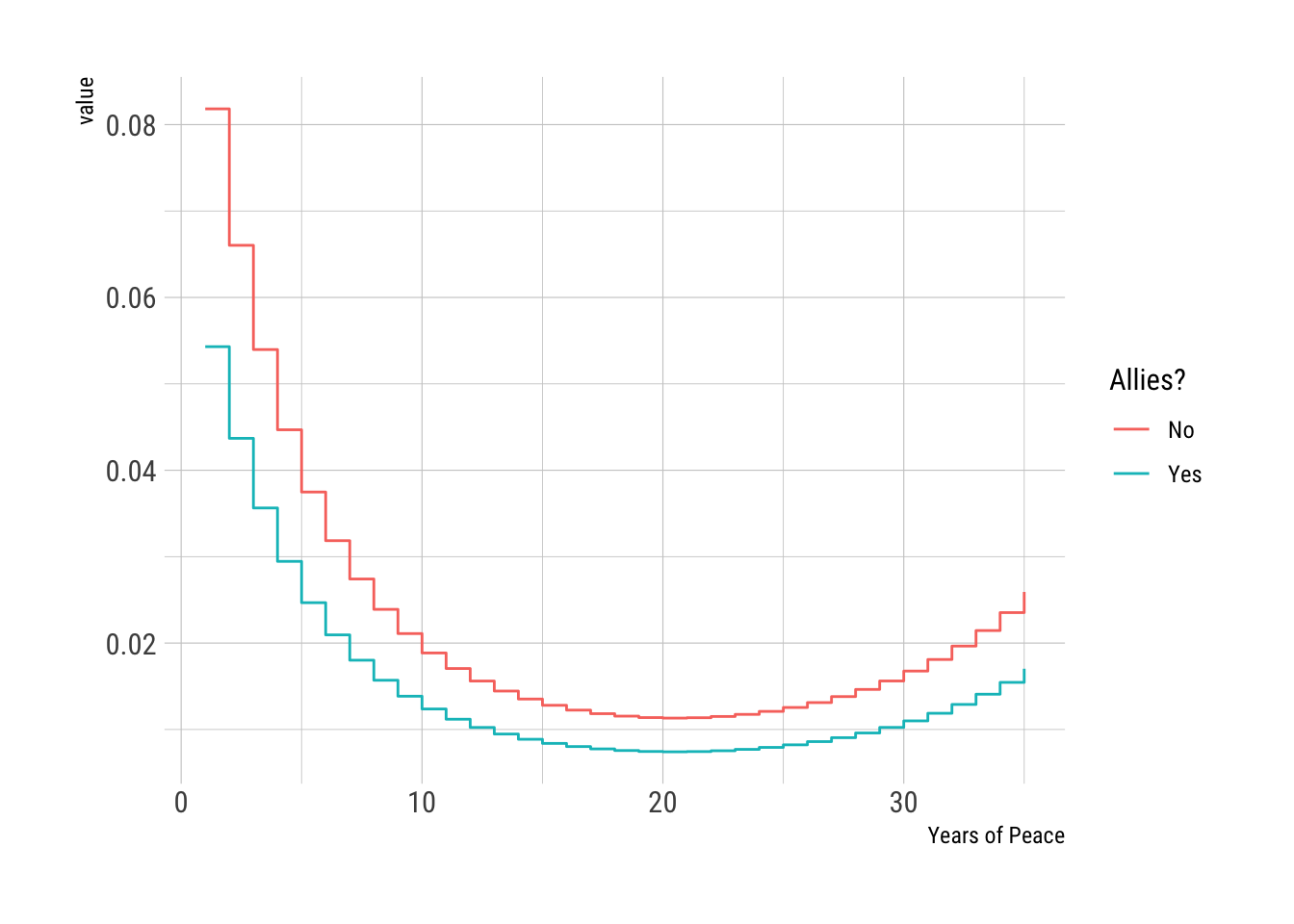
```{r}
Scenario.1 <- data.frame(dem = 0, growth=0, allies=0, contig=1, capratio=1, trade=0.002, py=seq(1,35))
Scenario.2 <- data.frame(dem = 0, growth=0, allies=1, contig=1, capratio=1, trade=0.002, py=seq(1,35))
Res.1 <- predict(cloglog_model, newdata=Scenario.1, type= "response")
Res.2 <- predict(cloglog_model, newdata=Scenario.2, type= "response")
data.frame(No = Res.1, Yes = Res.2, Scenario.1) %>% pivot_longer(., cols=c(No, Yes)) %>% ggplot() + aes(x=py, y=value, color=name) + labs(x="Years of Peace", color="Allies?") + geom_step() + hrbrthemes::theme_ipsum_rc()
```
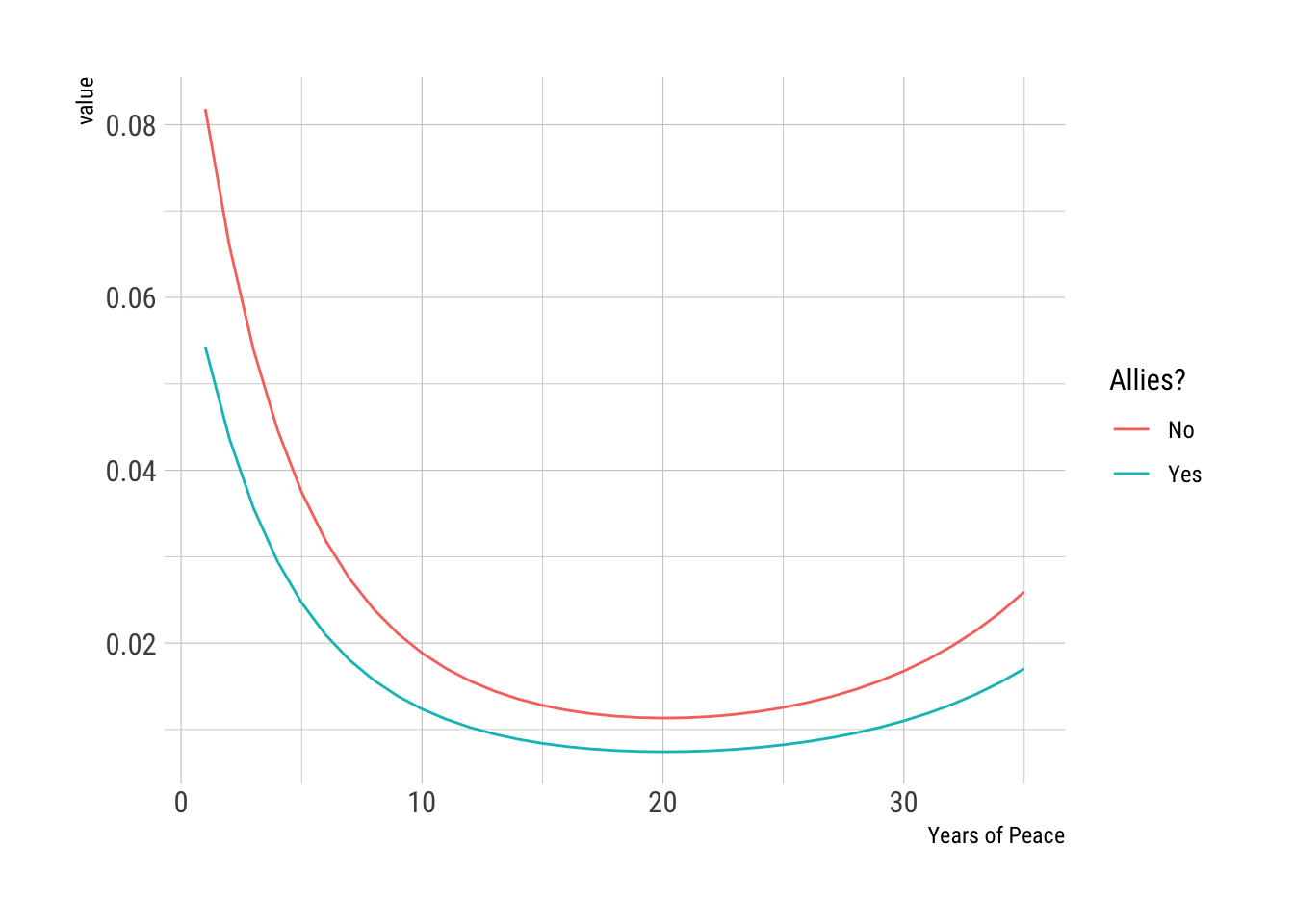
geom_line smooths it out
```{r}
Scenario.1 <- data.frame(dem = 0, growth=0, allies=0, contig=1, capratio=1, trade=0.002, py=seq(1,35))
Scenario.2 <- data.frame(dem = 0, growth=0, allies=1, contig=1, capratio=1, trade=0.002, py=seq(1,35))
Res.1 <- predict(cloglog_model, newdata=Scenario.1, type= "response")
Res.2 <- predict(cloglog_model, newdata=Scenario.2, type= "response")
data.frame(No = Res.1, Yes = Res.2, Scenario.1) %>% pivot_longer(., cols=c(No, Yes)) %>% ggplot() + aes(x=py, y=value, color=name) + labs(x="Years of Peace", color="Allies?") + geom_line() + hrbrthemes::theme_ipsum_rc()
```