Hubbard’s Rule of Five

R
binomial
Author

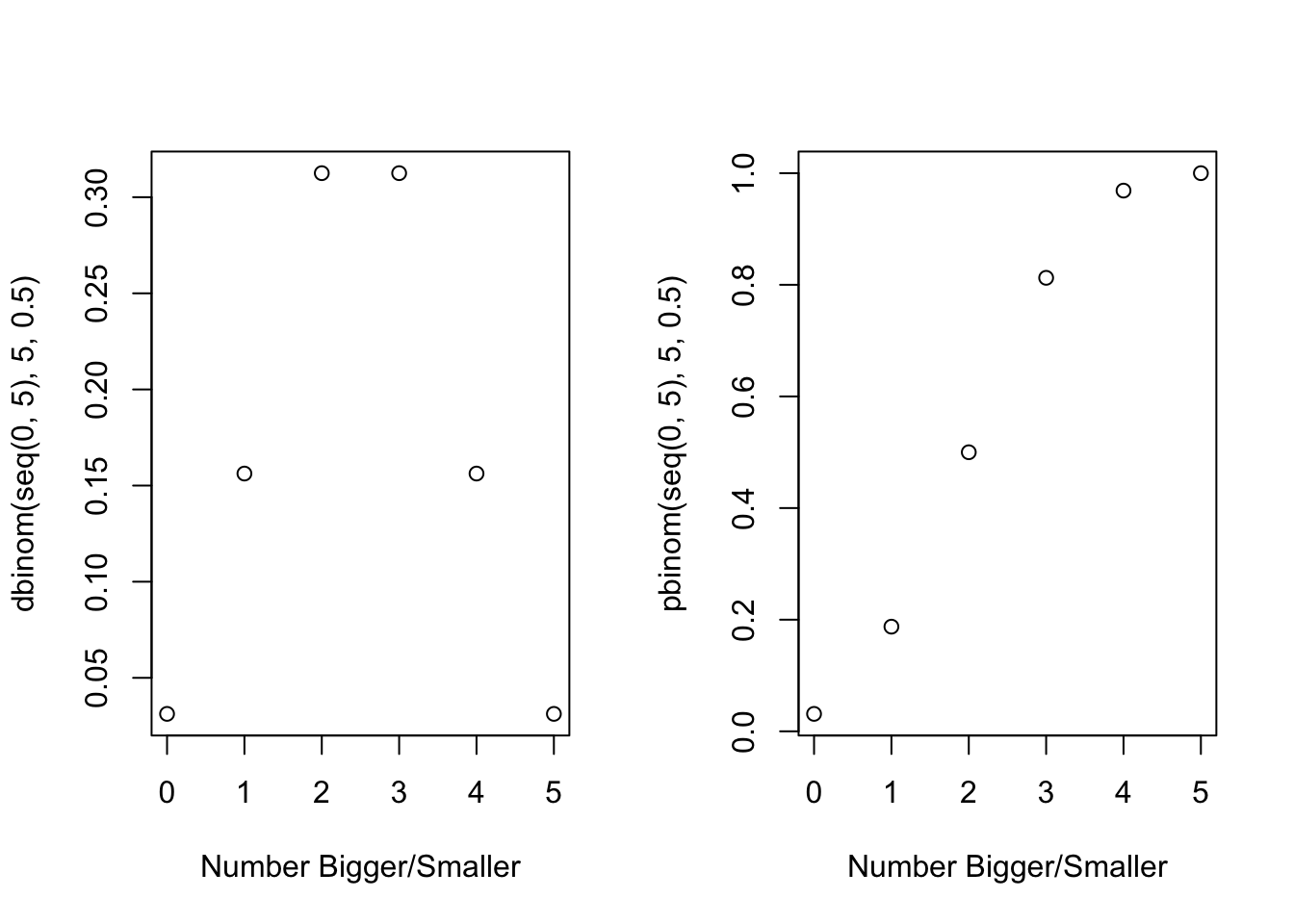
Robert W. Walker

Published

February 5, 2023

Rule of Five

The Rule of Five states that the median of any population should be between the lowest and highest collected values in a sample of five with almost 94 percent probability. Why?

  1. The probability of any given observation being above or below the median is 0.5 each.
  2. With a sample of size 5, let’s plot the relevant binomial.

Binomial Plots

par(mfrow=c(1,2))
plot(x=seq(0,5), y=dbinom(seq(0,5), 5, 0.5), xlab="Number Bigger/Smaller")
plot(x=seq(0,5), y=pbinom(seq(0,5), 5, 0.5), xlab="Number Bigger/Smaller")

A More Informative Plot

par(mfrow=c(1,1))
plot(x=seq(0,5), y=dbinom(seq(0,5), 5, 0.5), xlab="Number Bigger/Smaller", pch="", ylab="Binomial Prob. (5, 0.5)", xlim=c(-1,6))
text(x=seq(0,5), y=dbinom(seq(0,5), 5, 0.5), labels=round(dbinom(seq(0,5), 5, 0.5), digits=4))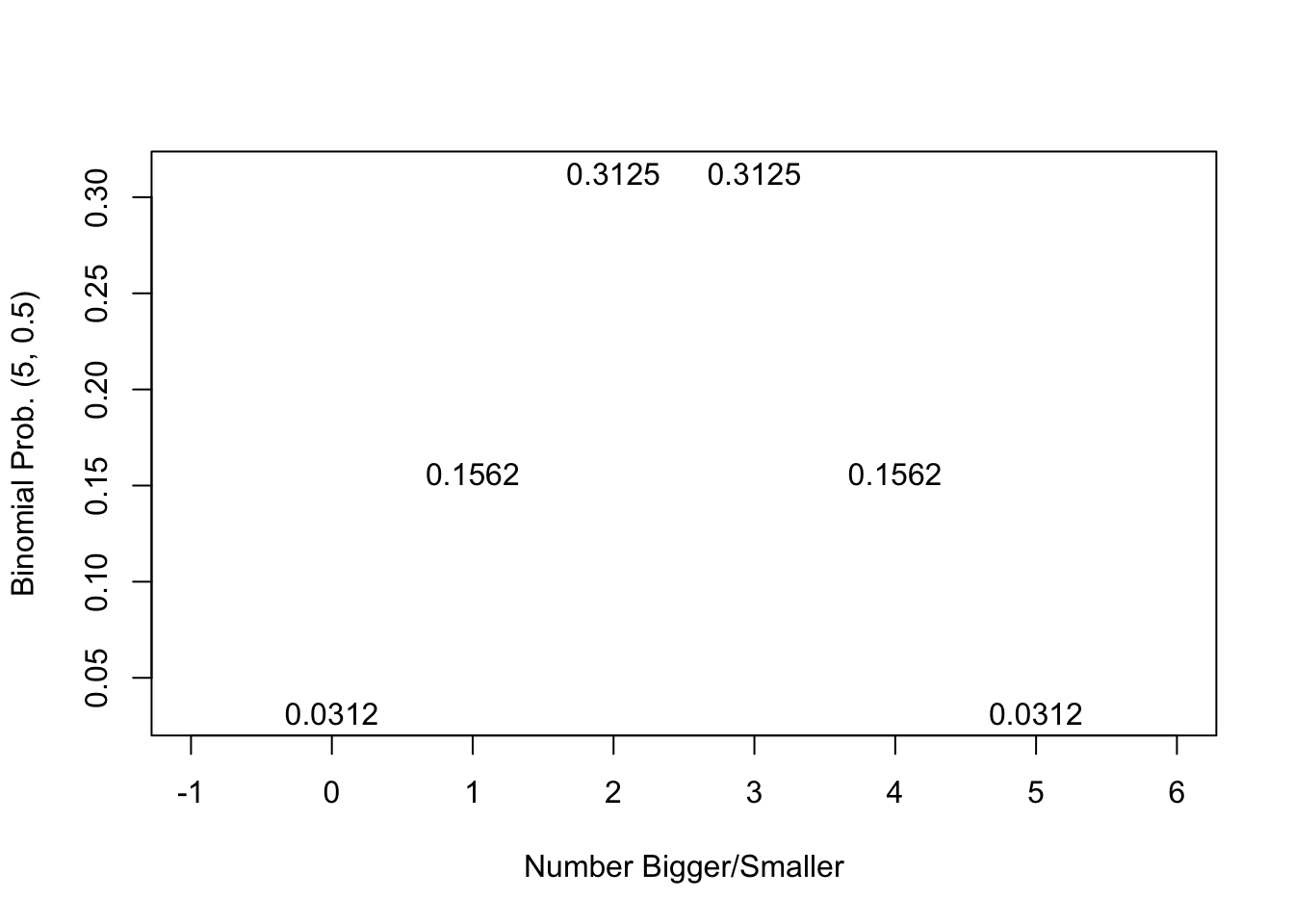

The probability that all five observations are above [0.03125] or below [0.03125] totals to 0.0625; there is a 93.75% chance it is interior to the five random observations.

References

Hubbard, D. W. 2010. How to Measure Anything: Finding the Value of Intangibles in Business. Wiley. https://books.google.com/books?id=CBAh4eM-g3AC.