Discrete Distributions

Linking Probability and Data

Robert W. Walker

Discrete Distributions

Code

library(tidyverse)
theme_set(theme_minimal())

Probability Distributions of Two Forms

Our core concept is a probability distribution just as above. These come in two forms for two types [discrete (qualitative)] and continuous (quantitative)] and can be either:

Assumed, or
Derived

The Poster and Examples

Distributions are nouns.
Sentences are incomplete without verbs – parameters.
We need both; it is for this reason that the former slide is true.
We do not always have a grounding for either the name or the parameter.
For now, we will work with univariate distributions though multivariate distributions do exist.

Functions

Probability distributions are mathematical formulae expressing likelihood for some set of qualities or quantities.

They have names: nouns.
They also have verbs: parameters.

Like a proper English sentence, both are required.

Models

What is a model?

For our purposes, it is a systematic description of a phenomenon that shares important and essential features of that phenomenon. Models frequently give us leverage on problems in the absence of alternative approaches.

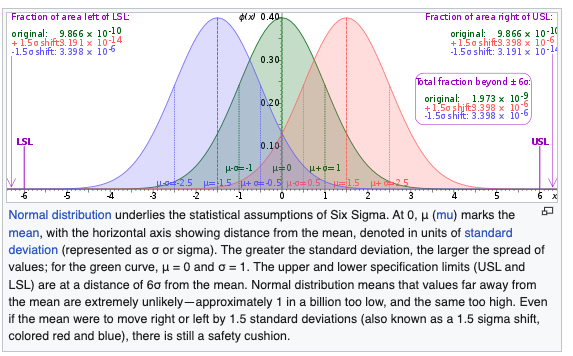
One Review Problem: Six Sigma

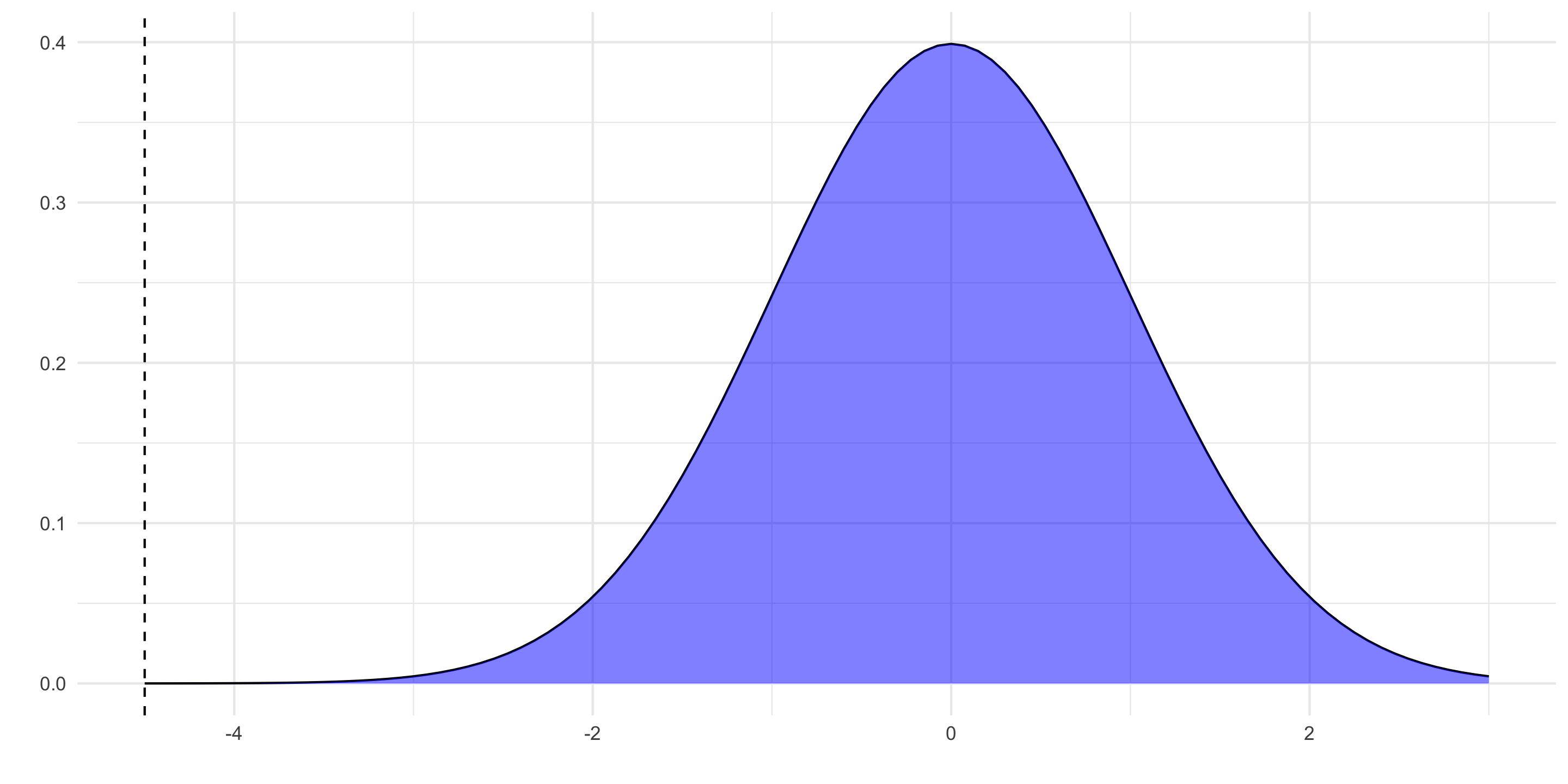
6\sigma is a widely used tool in TQM [total quality management]. But 6\sigma isn’t actually 6\sigma. The famous mantra that goes with it is 3.4 dipmo [defects per million opportunities]. This means that the outer limit [and it only considers one-sided/tailed] on defects is 0.0000034.

Radiant on the problem.

Code

options(scipen=8)
library(radiant)
result <- prob_norm(mean = 0, stdev = 1, plb = 0.0000034)
summary(result, type = "probs")

Probability calculator
Distribution: Normal
Mean        : 0 
St. dev     : 1 
Lower bound : 0.0000034 
Upper bound : 1 

P(X < -4.5) = 0.0000034
P(X > -4.5) = 1

6\sigma is only 4.5.

Code

plot(result, type = "probs") + theme_minimal()

Today’s Models

The Poisson will be defined an arrival rate \lambda – lambda.
Bernoulli trials: Two outcomes occur with probability \pi and 1-\pi.
- The binomial distribution will be defined by a number of trials n and a probability \pi.
- The geometric distribution defines the first success of n trials with probability \pi.
- The negative binomial distribution defines the probability of k successes in n trials with probability \pi. It is related to the Poisson.

Events: The Poisson

Poisson

Take a binomial with p very small and let n \rightarrow \infty. We get the Poisson distribution (y) given an arrival rate \lambda specified in events per period.

f(y|\lambda) = \frac{\lambda^{y}e^{-\lambda}}{y!}

Examples: The Poisson

Walk in customers
Emergency Room Arrivals
Births, deaths, marriages
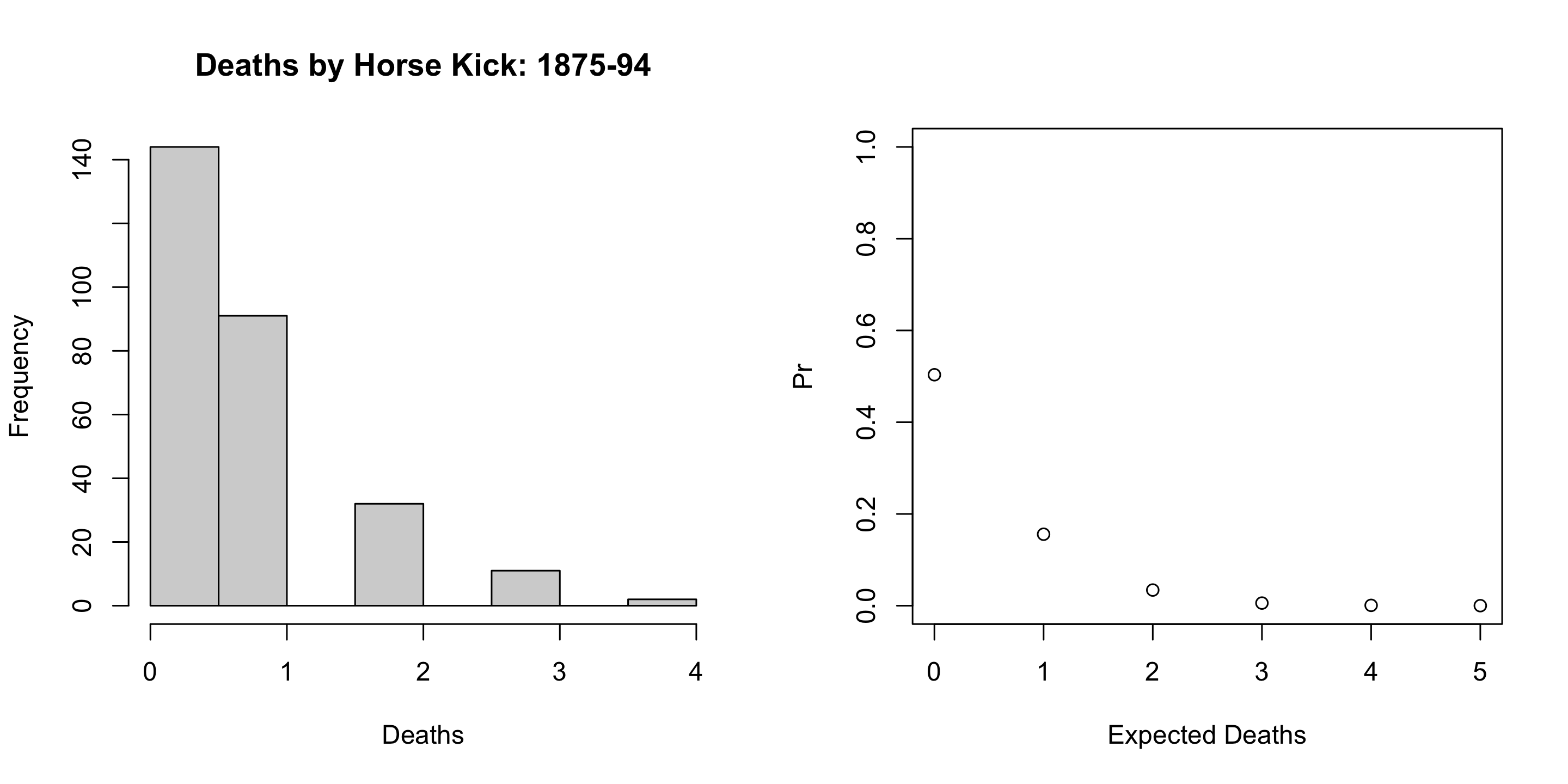
Prussian Cavalry Deaths by Horse Kick
Fish?

Air Traffic Controllers

FAA Decision: Expend or do not expend scarce resources investigating claimed staffing shortages at the Cleveland Air Route Traffic Control Center.

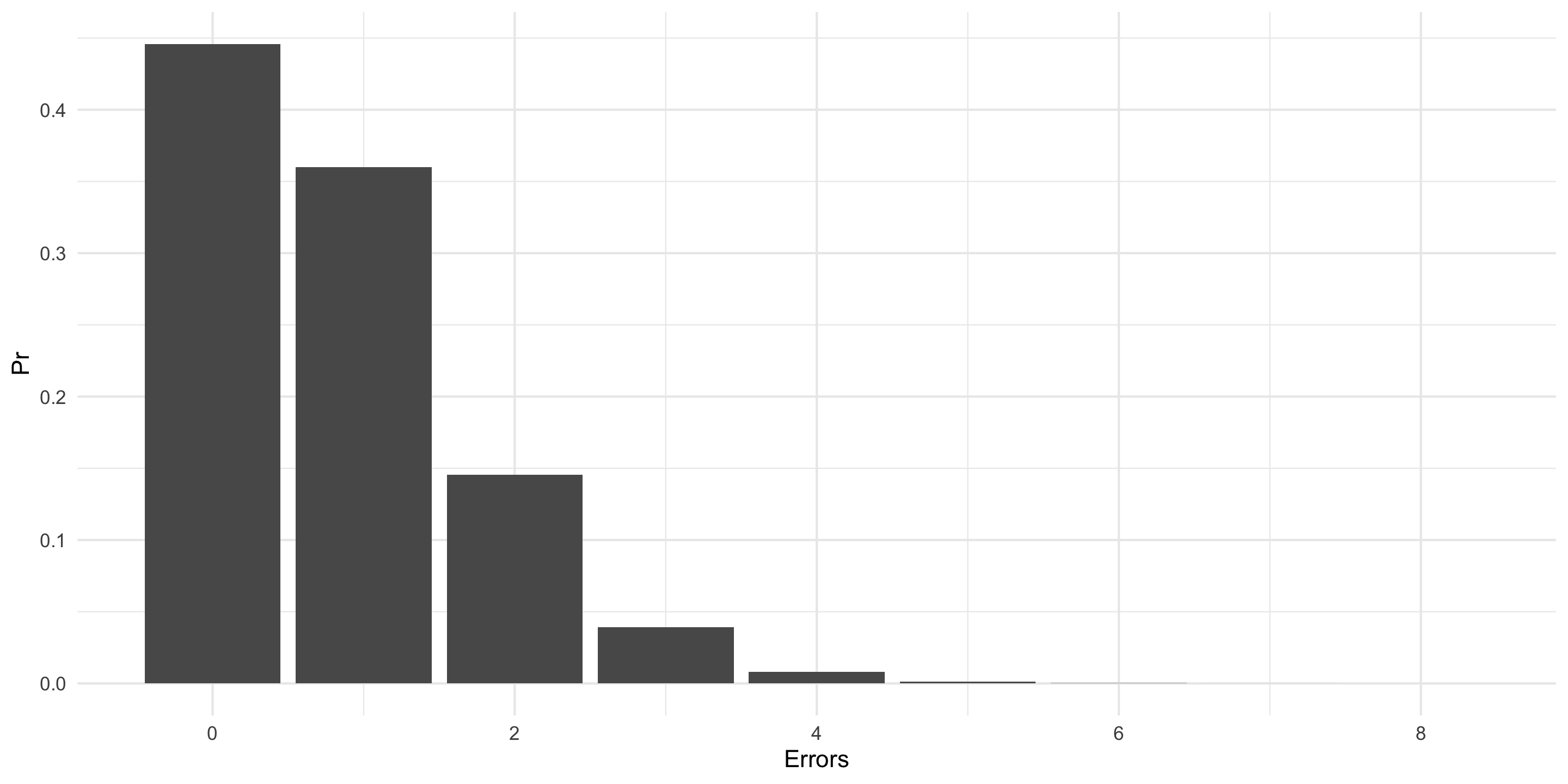
Essential facts: The Cleveland ARTCC is the US’s busiest in routing cross-country air traffic. In mid-August of 1998, it was reported that the first week of August experienced 3 errors in a one week period; an error occurs when flights come within five miles of one another by horizontal distance or 2000 feet by vertical distance. The Controller’s union claims a staffing shortage though other factors could be responsible. 21 errors per year (21/52 [0.4038462] errors per week) has been the norm in Cleveland for over a decade.

Some Questions

Plot a histogram of 1000 random weeks. NB: pois is the noun with no default for \lambda – the arrival rate.

Code

DF <- data.frame(Close.Calls = rpois(1000, 21/52))
ggplot(DF) + aes(x=Close.Calls) + geom_histogram()

Code

ggplot(DF) + aes(x=Close.Calls) + stat_ecdf(geom="step")

Another Look

Plot a sequence on the x axis from 0 to 5 and the probability of that or fewer incidents along the y. seq(0,5)

Code

DF <- data.frame(x=0:5, y=ppois(0:5, 21/52))
ggplot(DF) + aes(x=x, y=y) + geom_col()

Decision

What would you do and why? Not impossible. The probability of this number or greater is 0.0081342

A Wrinkle

After analyzing the initial data, you discover that the first two weeks of August have experienced 6 errors. What would you now decide?

Well, once is 0.0081342. Twice, at random, is that squared. We have a problem. Or…

Code

data.frame(Errors = seq(0,8)) %>% mutate(Pr = dpois(Errors, 21/26)) %>% ggplot() + aes(x=Errors, y=Pr) + geom_col() + theme_minimal()

Deaths by Horse Kick in the Prussian cavalry?

Code

library(vcd)
data(VonBort)
head(VonBort)

  deaths year corps fisher
1      0 1875     G     no
2      0 1875     I     no
3      0 1875    II    yes
4      0 1875   III    yes
5      0 1875    IV    yes
6      0 1875     V    yes

In Von Bortkiewicz’s data, the average number of deaths by horse kick is:

Code

mean(VonBort$deaths)

[1] 0.7

Bernoulli Trials

The Generic Bernoulli Trial

Suppose the variable of interest is discrete and takes only two values: yes and no. For example, is a customer satisfied with the outcomes of a given service visit?

For each individual, because the probability of yes (1) \pi and no (0) 1-\pi must sum to one, we can write:

f(x|\pi) = \pi^{x}(1-\pi)^{1-x}

Binomial Distribution

For multiple identical trials, we have the Binomial:

f(x|n,\pi) = {n \choose k} \pi^{x}(1-\pi)^{n-x} where {n \choose k} = \frac{n!}{(n-k)!}

The Binomial

BinomialR

Scottish Pounds

Informal surveys suggest that 15% of Essex shopkeepers will not accept Scottish pounds. There are approximately 200 shops in the general High Street square.

Draw a plot of the distribution and the cumulative distribution of shopkeepers that do not accept Scottish pounds.

Code

Scots <- data.frame(Potential.Refusers = 0:200) %>% mutate(Prob = round(pbinom(Potential.Refusers, size=200, 0.15), digits=4))
Scots %>% ggplot() + aes(x=Potential.Refusers, y=Prob) + geom_point() + labs(x="Refusers", y="Prob. of x or Less Refusers") + theme_minimal() -> Plot1
Plot1

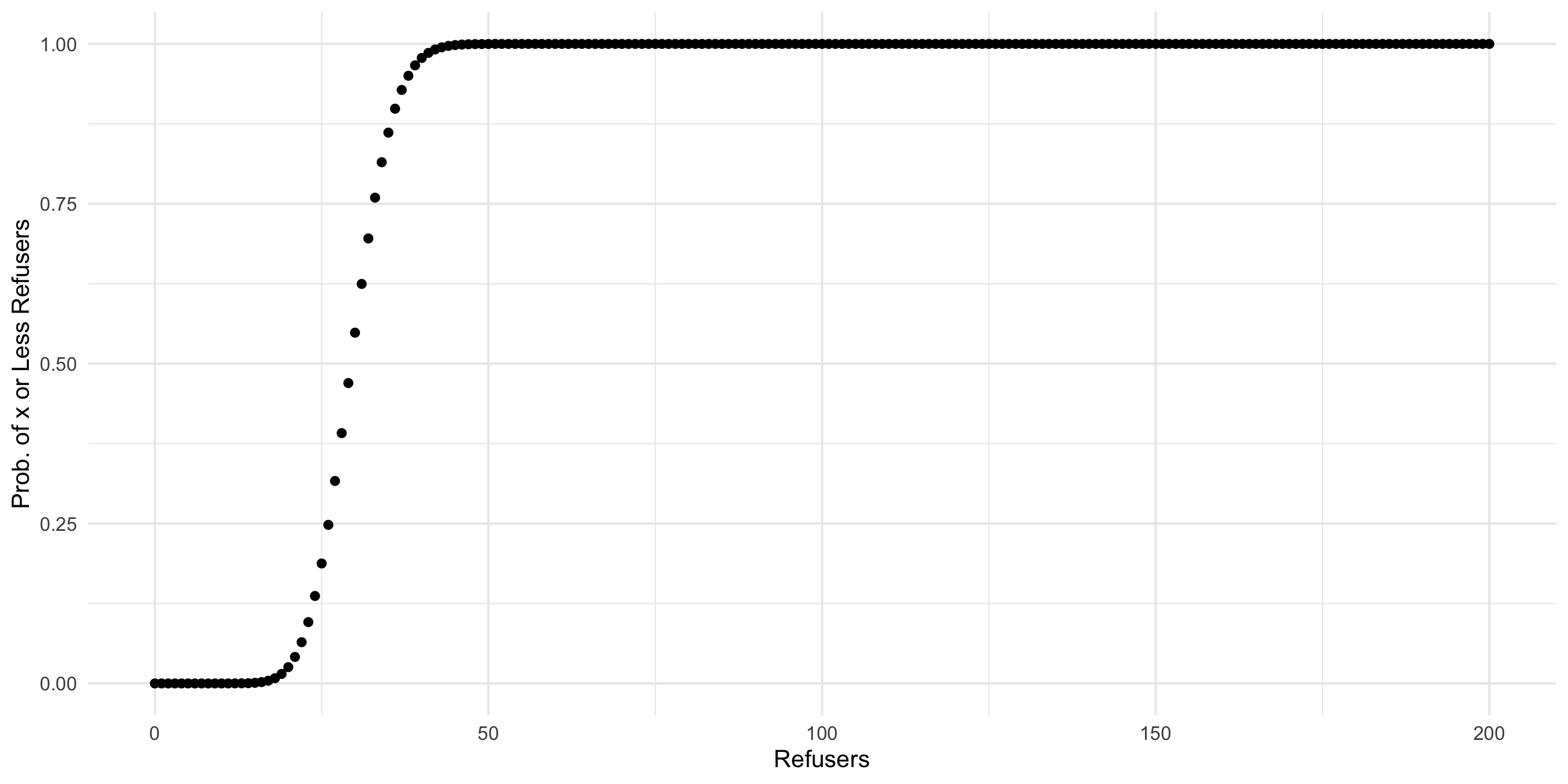
A Nicer Plot

Code

library(plotly)
p <- ggplotly(Plot1)
p

Even More Scottish Pounds

With probability 0.9 [90 percent], XXX or fewer shopkeepers will not accept Scottish pounds.

Code

qbinom(0.9, 200, 0.15)

[1] 37

The Median is a Binomial with p=0.5

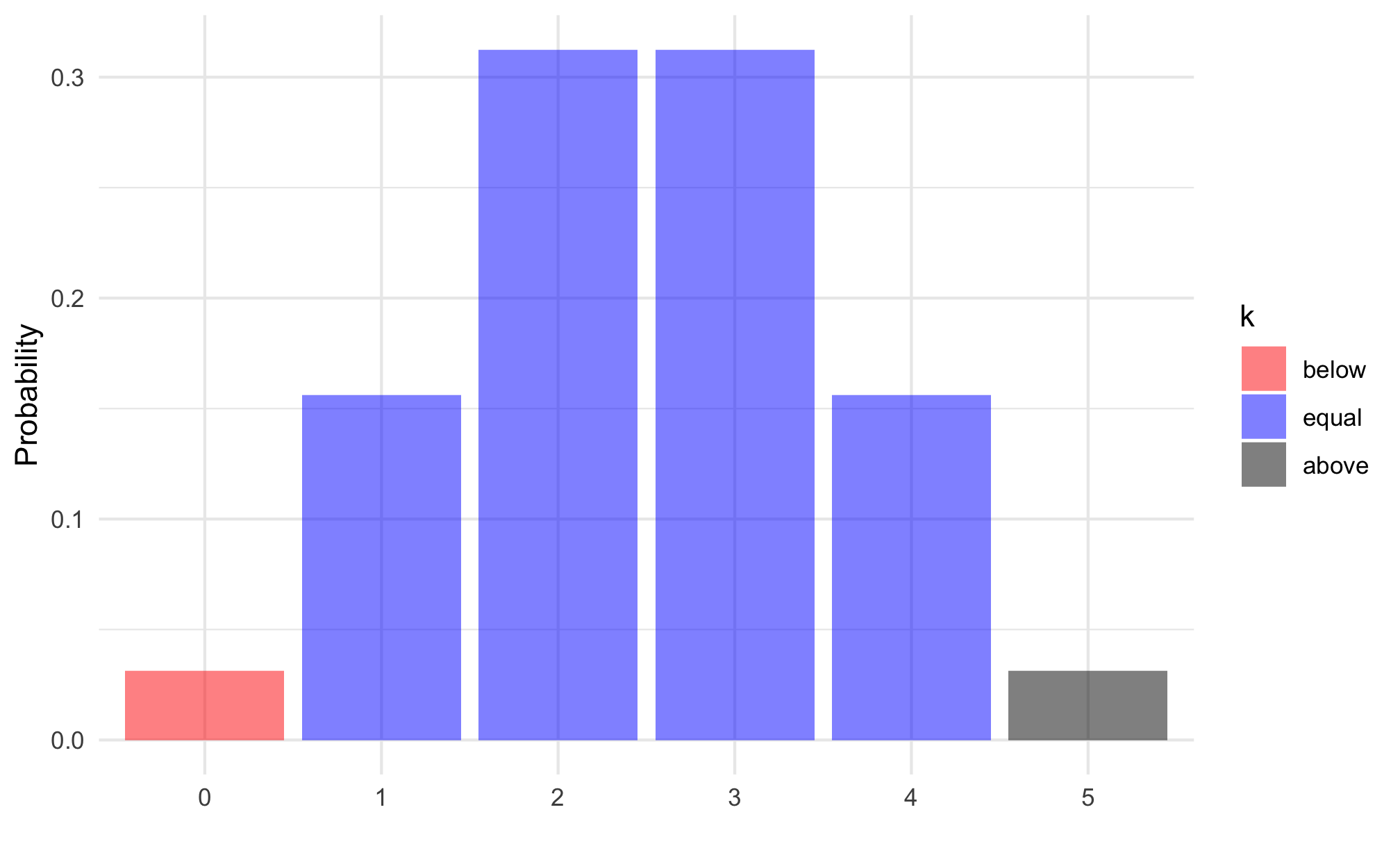
Interestingly, any given observation has a 50-50 chance of being over or under the median. Suppose that I have five datum.

What is the probability that all are under?

Code

pbinom(0,size=5, p=0.5)

[1] 0.03125

What is the probability that all are over?

Code

dbinom(5,size=5, p=0.5)

[1] 0.03125

What is the probability that the median is somewhere in between our smallest and largest sampled values?

Everything else.

1 - 0.03125 - 0.03125 = 0.9375

Code

result <- prob_binom(n = 5, p = 0.5, lb = 1, ub = 4)
plot(result) + theme_minimal()

The Rule of Five

This is called the Rule of Five by Hubbard in his How to Measure Anything.

Geometric Distributions

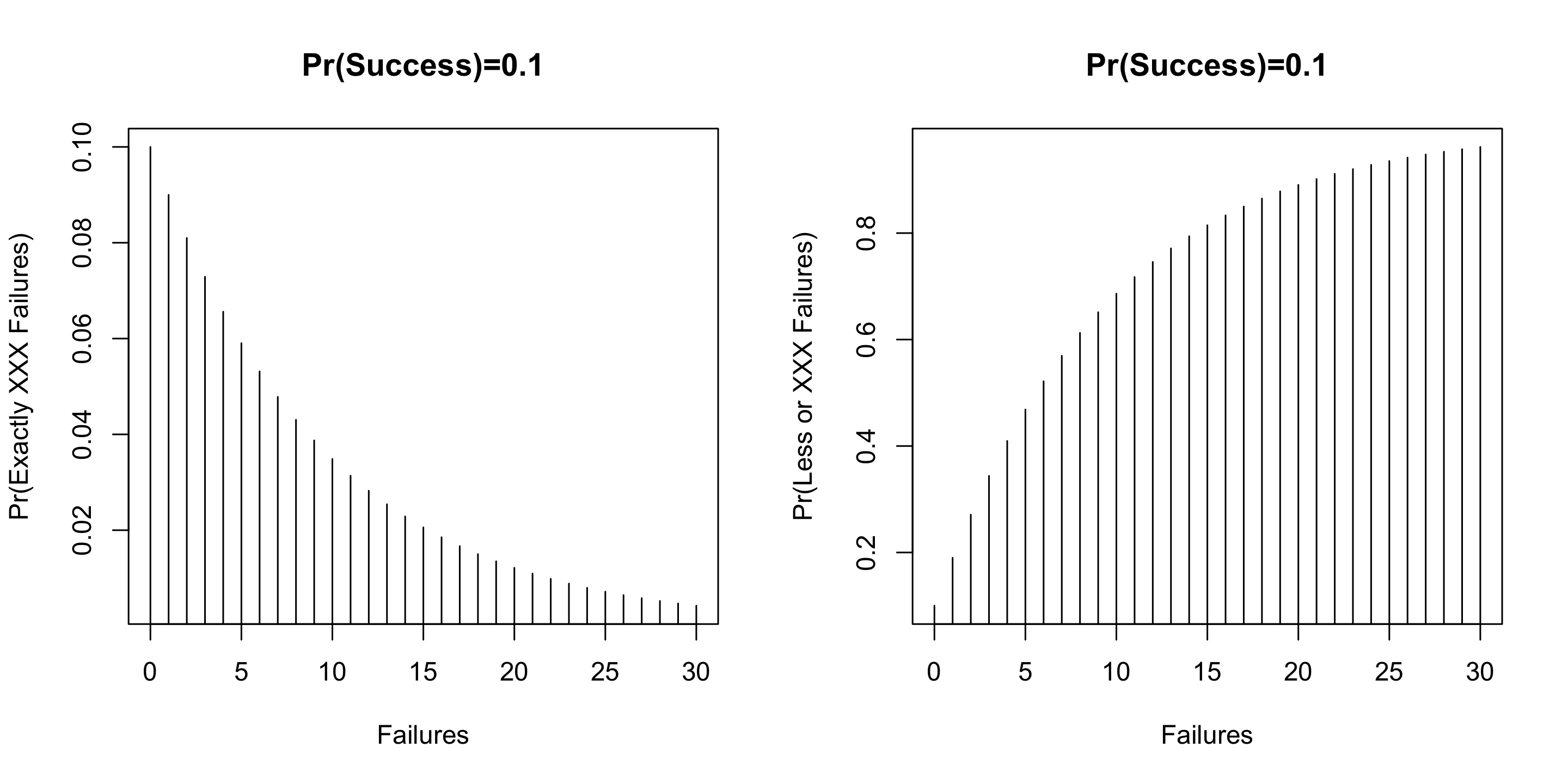
How many failures before the first success? Now defined exclusively by p. In each case, (1-p) happens k times. Then, on the k+1^{th} try, p. Note 0 failures can happen…

Pr(y=k) = (1-p)^{k}p

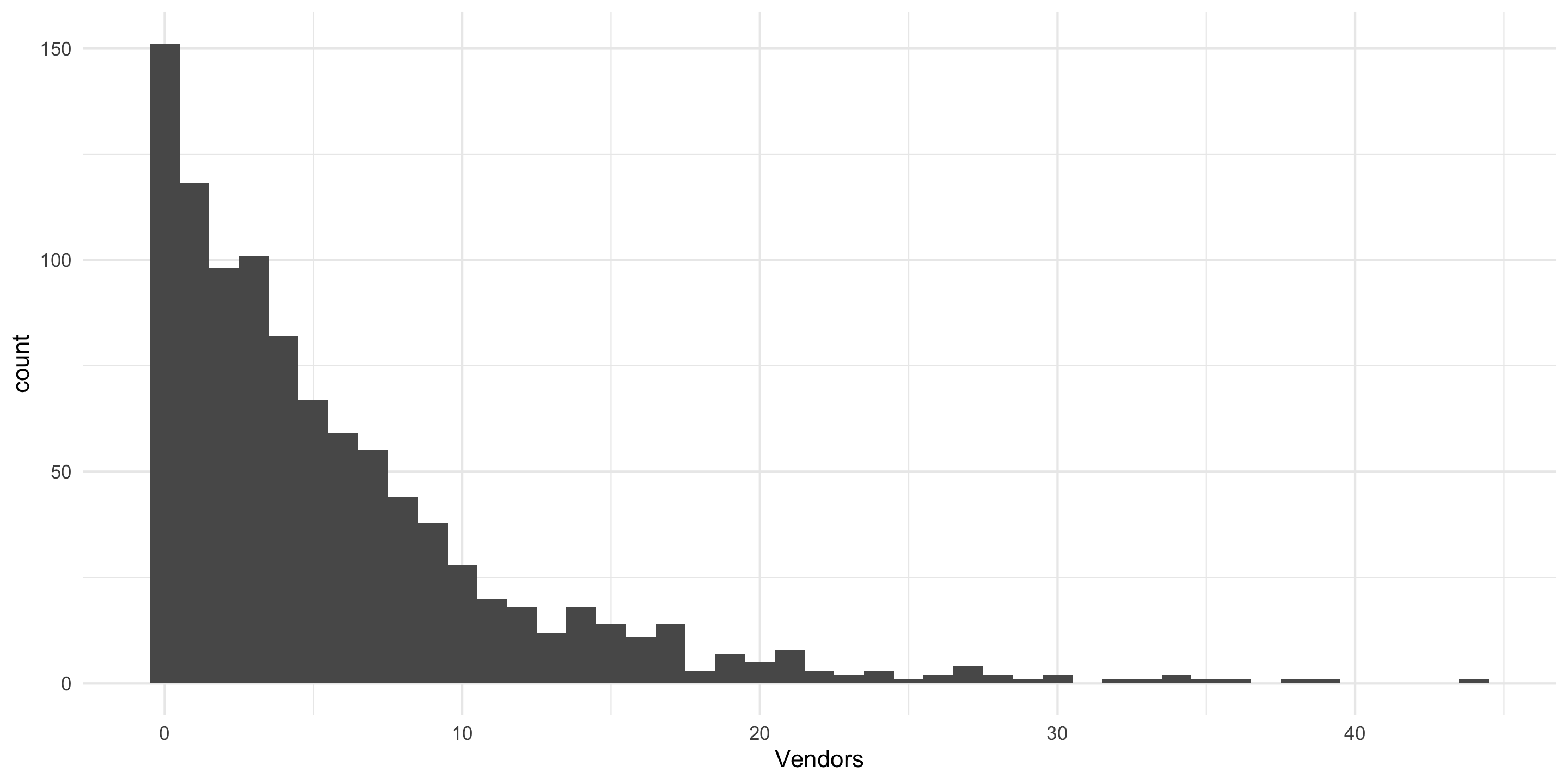
Example: Entrepreneurs

Suppose any startup has a p=0.1 chance of success. How many failures?

Suppose any startup has a p=0.1 chance of success. How many failures for the average/median person?

Code

qgeom(0.5,0.1)

[1] 6

Example: Entrepreneurs

[Geometric] Plot 1000 random draws of “How many vendors until one refuses my Scottish pounds?”

Code

Geoms.My <- data.frame(Vendors=rgeom(1000, 0.15))
Geoms.My %>% ggplot() + aes(x=Vendors) + geom_histogram(binwidth=1)

We could also do something like.

Code

Plotly.Me <- data.frame(Refuseniks = seq(0,60), Pr = pgeom(seq(0,60), 0.15)) %>% ggplot() + aes(x=Refuseniks, y=Pr) + geom_col()
ggplotly(Plotly.Me)

Negative Binomial Distributions

How many failures before the r^{th} success? In each case, (1-p) happens k times. Then, on the k+1^{th} try, we get our r^{th} p. Note 0 failures can happen…

Pr(y=k) = {k+r-1 \choose r-1}(1-p)^{k}p^{r}

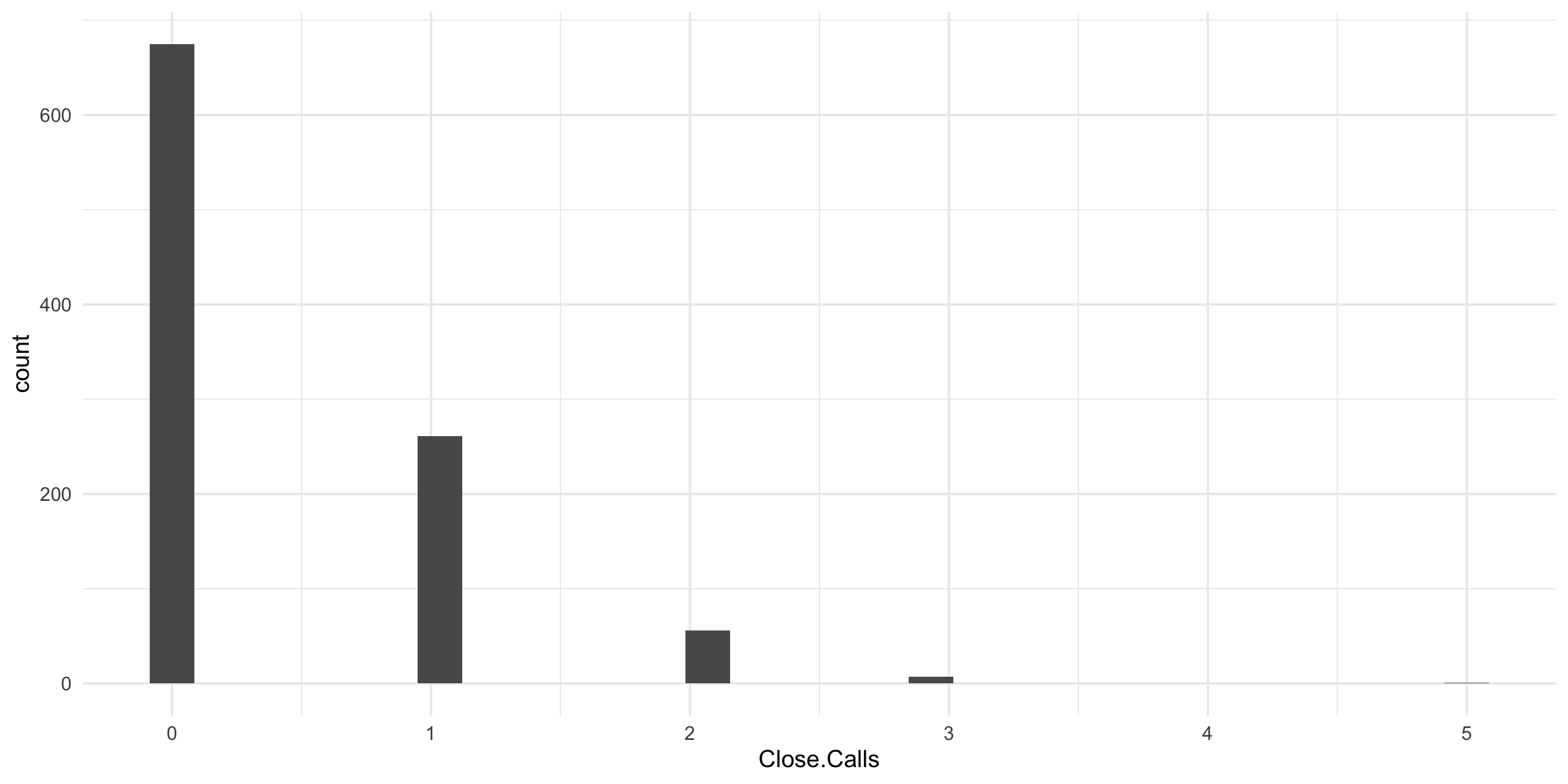
Needed Sales

I need to make 5 sales to close for the day. How many potential customers will I have to have to get those five sales when each customer purchases with probability 0.2.

Code

library(patchwork)
DF <-  data.frame(Customers = c(0:70)) %>% 
  mutate(m.Customers = dnbinom(Customers, size=5, prob=0.2), 
         p.Customers = pnbinom(Customers, size=5, prob=0.2)) 
pl1 <- DF %>% ggplot() + aes(x=Customers) + geom_line(aes(y=p.Customers))  + theme_minimal()
pl2 <- DF %>% ggplot() + aes(x=Customers) + geom_point(aes(y=m.Customers)) + theme_minimal()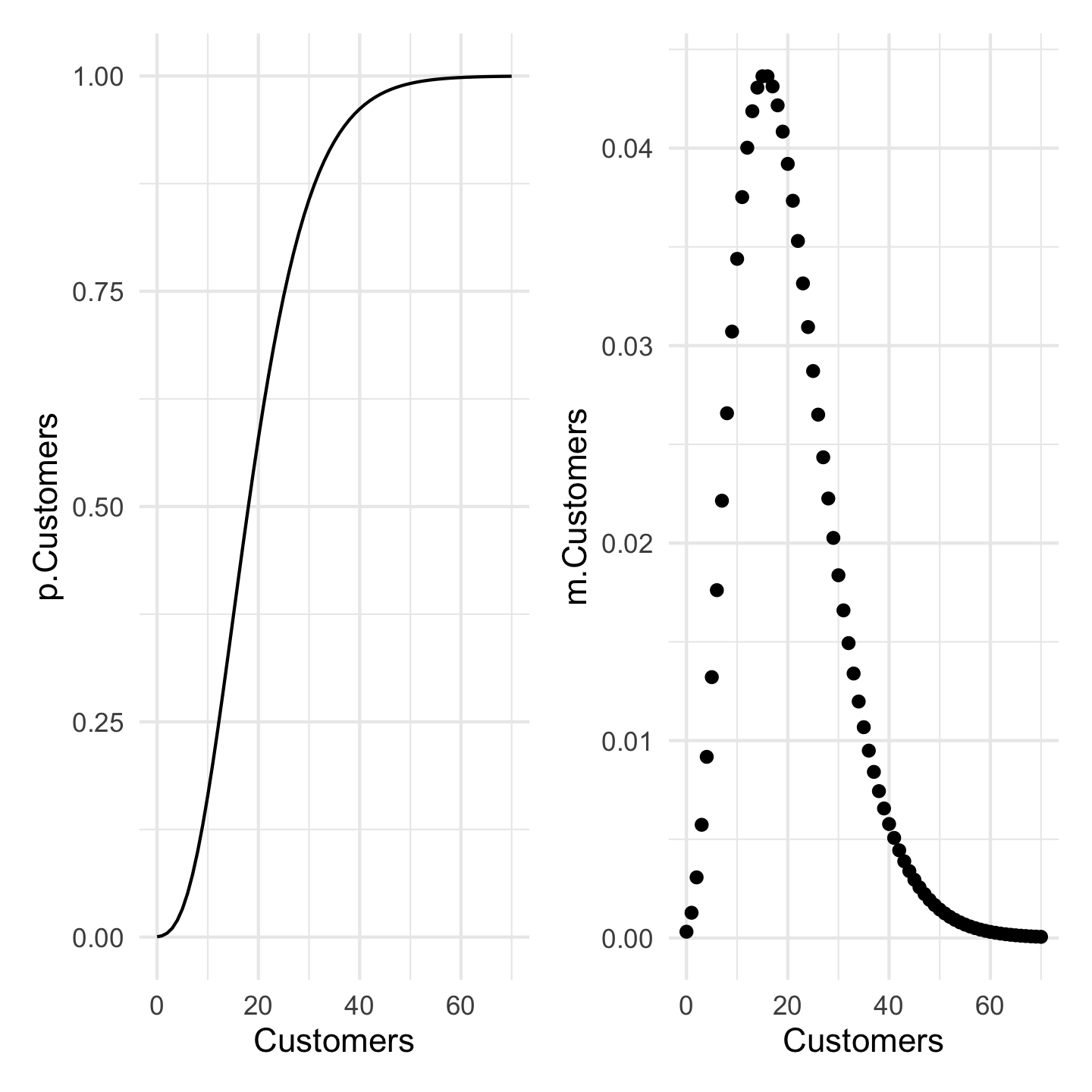

Simulation: A Powerful Tool

In this last example, I was concerned with sales. I might also want to generate revenues because I know the rough mean and standard deviation of sales. Combining such things together forms the basis of a Monte Carlo simulation.

Some of the basics are covered in a swirl on simulation.

An Example

Customers arrive at a rate of 7 per hour. You convert customers to buyers at a rate of 85%. Buyers spend, on average 600 dollars with a standard deviation of 150 dollars.

Code

Sim <- 1:1000
Customers <- rpois(1000, 7)
Buyers <- rbinom(1000, size=Customers, prob = 0.85)
Data <- data.frame(Sim, Buyers, Customers)
Data <- Data %>% group_by(Sim) %>% mutate(Revenue = sum(rnorm(Buyers, 600, 150))) %>% ungroup()

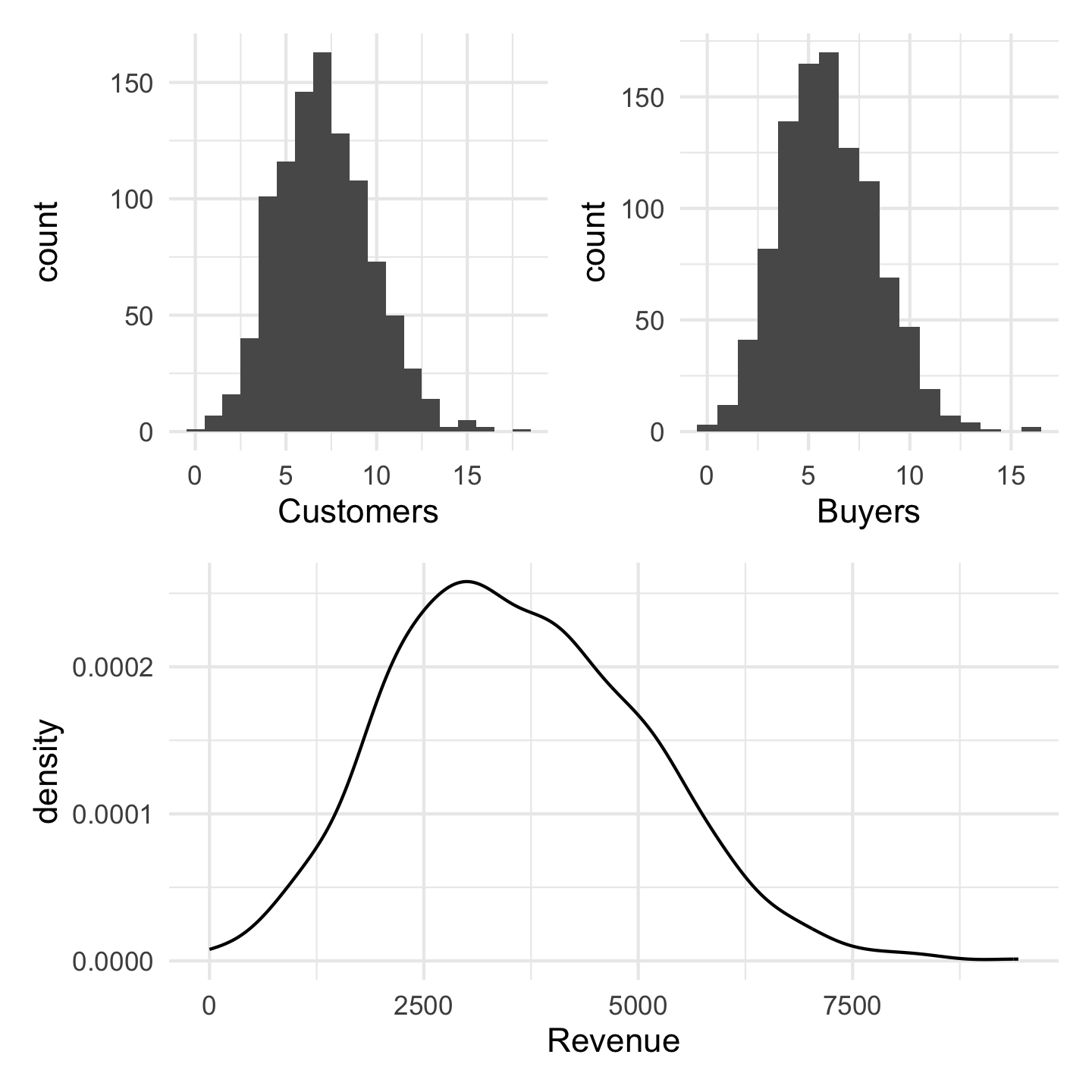
A Summary of Distributions

Distributions are how variables and probability relate. They are a graph that we can enter in two ways. From the probability side to solve for values or from values to solve for probability. It is always a function of the graph.

Distributions generally have to be sentences.

The name is a noun but it also has
parameters – verbs – that makes the noun tangible.

Discrete Distributions

Discrete Distributions

Probability Distributions of Two Forms

The Poster and Examples

Functions

Models

What is a model?

One Review Problem: Six Sigma

Radiant on the problem.

Today’s Models

Events: The Poisson

Examples: The Poisson

Air Traffic Controllers

Some Questions

Another Look

Decision

A Wrinkle

Deaths by Horse Kick in the Prussian cavalry?

Bernoulli Trials

The Generic Bernoulli Trial

Binomial Distribution

The Binomial

Scottish Pounds

A Nicer Plot

More Questions About Scottish Pounds

Even More Scottish Pounds

The Median is a Binomial with p=0.5

The Rule of Five

Geometric Distributions

Example: Entrepreneurs

Example: Entrepreneurs

Negative Binomial Distributions

Needed Sales

Simulation: A Powerful Tool

An Example

A Summary of Distributions